作者丨苏剑林
单位丨广州火焰信息科技有限公司
研究方向丨NLP,神经网络
个人主页丨kexue.fm
前言
2017 年中,有两篇类似同时也是笔者非常欣赏的论文,分别是 FaceBook 的 Convolutional Sequence to Sequence Learning 和 Google 的 Attention is All You Need,它们都算是 Seq2Seq 上的创新,本质上来说,都是抛弃了 RNN 结构来做 Seq2Seq 任务。
在本篇文章中,笔者将对 Attention is All You Need 做一点简单的分析。当然,这两篇论文本身就比较火,因此网上已经有很多解读了(不过很多解读都是直接翻译论文的,鲜有自己的理解),因此这里尽可能多自己的文字,尽量不重复网上各位大佬已经说过的内容。
序列编码
深度学习做 NLP 的方法,基本上都是先将句子分词,然后每个词转化为对应的词向量序列。这样一来,每个句子都对应的是一个矩阵 X=(x1,x2,…,xt),其中 xi 都代表着第 i 个词的词向量(行向量),维度为 d 维,故
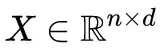
请点击此处输入图片描述
。这样的话,问题就变成了编码这些序列了。第一个基本的思路是 RNN 层,RNN 的方案很简单,递归式进行:
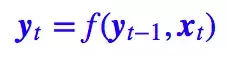
请点击此处输入图片描述
不管是已经被广泛使用的 LSTM、GRU 还是最近的 SRU,都并未脱离这个递归框架。RNN 结构本身比较简单,也很适合序列建模,但 RNN 的明显缺点之一就是无法并行,因此速度较慢,这是递归的天然缺陷。
另外我个人觉得 RNN 无法很好地学习到全局的结构信息,因为它本质是一个马尔科夫决策过程。
第二个思路是 CNN 层,其实 CNN 的方案也是很自然的,窗口式遍历,比如尺寸为 3 的卷积,就是:

请点击此处输入图片描述
在 FaceBook 的论文中,纯粹使用卷积也完成了 Seq2Seq 的学习,是卷积的一个精致且极致的使用案例,热衷卷积的读者必须得好好读读这篇文论。
CNN 方便并行,而且容易捕捉到一些全局的结构信息,笔者本身是比较偏爱 CNN 的,在目前的工作或竞赛模型中,我都已经尽量用 CNN 来代替已有的 RNN 模型了,并形成了自己的一套使用经验,这部分我们以后再谈。
Google的大作提供了 第三个思路:纯 Attention, 单靠注意力就可以。
RNN 要逐步递归才能获得全局信息,因此一般要双向 RNN 才比较好;CNN 事实上只能获取局部信息,是通过层叠来增大感受野;Attention 的思路最为粗暴,它一步到位获取了全局信息,它的解决方案是:
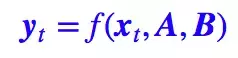
请点击此处输入图片描述
其中 A,B 是另外一个序列(矩阵)。如果都取 A=B=X,那么就称为 Self Attention, 它的意思是直接将 xt 与原来的每个词进行比较,最后算出 yt。
Attention 定义
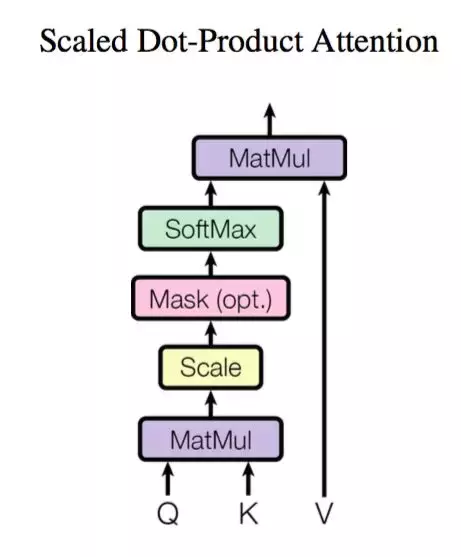
Google 的一般化 Attention 思路也是一个编码序列的方案,因此我们也可以认为它跟 RNN、CNN 一样,都是一个序列编码的层。
请点击此处输入图片描述
前面给出的是一般化的框架形式的描述,事实上 Google 给出的方案是很具体的。首先,它先把 Attention 的定义给了出来:
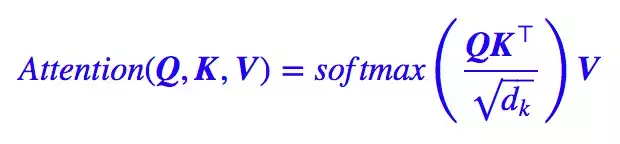
请点击此处输入图片描述
这里用的是跟 Google 的论文一致的符号,其中:

请点击此处输入图片描述
于是我们可以认为:这是一个 Attention 层, 将 n×dk 的序列 Q 编码成了一个新的 n×dv 的序列。
那怎么理解这种结构呢?我们不妨逐个向量来看。

请点击此处输入图片描述
其中 Z 是归一化因子。事实上 q,k,v 分别是 query,key,value 的简写,K,V 是一一对应的,它们就像是 key-value 的关系,那么上式的意思就是通过 qt 这个 query,通过与各个 ks 内积的并 softmax 的方式,来得到 qt 与各个 vs 的相似度,然后加权求和,得到一个 dv 维的向量。
其中因子
![]() 起到调节作用,使得内积不至于太大(太大的话 softmax 后就非 0 即 1 了,不够“soft”了)。
起到调节作用,使得内积不至于太大(太大的话 softmax 后就非 0 即 1 了,不够“soft”了)。
请点击此处输入图片描述
事实上这种 Attention 的定义并不新鲜,但由于 Google 的影响力,我们可以认为现在是更加正式地提出了这个定义,并将其视为一个层地看待。
此外这个定义只是注意力的一种形式,还有一些其他选择,比如 query 跟 key 的运算方式不一定是点乘(还可以是拼接后再内积一个参数向量),甚至权重都不一定要归一化,等等。
Multi-Head Attention
这个是 Google 提出的新概念,是 Attention 机制的完善。
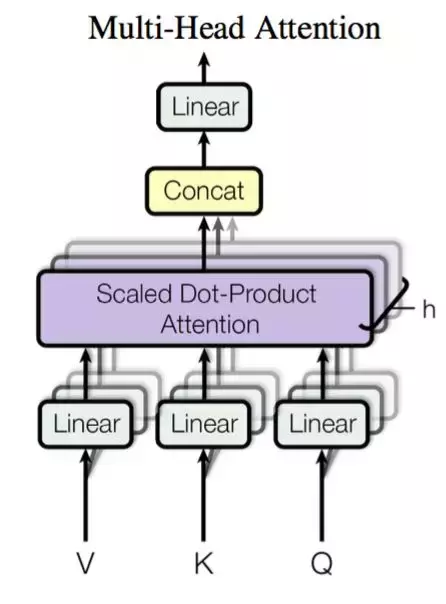
请点击此处输入图片描述
不过从形式上看,它其实就再简单不过了,就是把 Q,K,V 通过参数矩阵映射一下,然后再做 Attention,把这个过程重复做 h 次,结果拼接起来就行了,可谓“大道至简”了。具体来说:

请点击此处输入图片描述
这里
 ,
,
请点击此处输入图片描述

请点击此处输入图片描述
最后得到一个 n×(hd̃v) 的序列。 所谓“多头”(Multi-Head),就是只多做几次同样的事情(参数不共享),然后把结果拼接。
Self Attention
到目前为止,对 Attention 层的描述都是一般化的,我们可以落实一些应用。比如,如果做阅读理解的话, Q 可以是篇章的词向量序列,取 K=V 为问题的词向量序列,那么输出就是所谓的 Aligned Question Embedding。
而在 Google 的论文中,大部分的 Attention 都是 Self Attention, 即“自注意力”,或者叫内部注意力。
所谓 Self Attention,其实就是 Attention(X,X,X),X 就是前面说的输入序列。也就是说, 在序列内部做 Attention,寻找序列内部的联系。
Google 论文的主要贡献之一是 它表明了内部注意力在机器翻译(甚至是一般的 Seq2Seq 任务)的序列编码上是相当重要的,而之前关于 Seq2Seq 的研究基本都只是把注意力机制用在解码端。
类似的事情是,目前 SQUAD 阅读理解的榜首模型 R-Net 也加入了自注意力机制,这也使得它的模型有所提升。
当然,更准确来说,Google 所用的是 Self Multi-Head Attention:

请点击此处输入图片描述
Position Embedding
然而,只要稍微思考一下就会发现,这样的模型并不能捕捉序列的顺序。换句话说,如果将 K,V 按行打乱顺序(相当于句子中的词序打乱),那么 Attention 的结果还是一样的。
这就表明了, 到目前为止,Attention 模型顶多是一个非常精妙的“词袋模型”而已。
这问题就比较严重了,大家知道,对于时间序列来说,尤其是对于 NLP 中的任务来说,顺序是很重要的信息,它代表着局部甚至是全局的结构,学习不到顺序信息,那么效果将会大打折扣(比如机器翻译中,有可能只把每个词都翻译出来了,但是不能组织成合理的句子)。
于是 Google 再祭出了一招—— Position Embedding,也就是“位置向量”,将每个位置编号,然后每个编号对应一个向量,通过结合位置向量和词向量,就给每个词都引入了一定的位置信息,这样 Attention 就可以分辨出不同位置的词了。
Position Embedding 并不算新鲜的玩意,在 FaceBook 的 Convolutional Sequence to Sequence Learning 也用到了这个东西。但在 Google 的这个作品中,它的 Position Embedding 有几点区别:
1. 以前在 RNN、CNN 模型中其实都出现过 Position Embedding,但在那些模型中,Position Embedding 是锦上添花的辅助手段,也就是“有它会更好、没它也就差一点点”的情况,因为 RNN、CNN 本身就能捕捉到位置信息。
但是在这个纯 Attention 模型中,Position Embedding 是位置信息的唯一来源,因此它是模型的核心成分之一,并非仅仅是简单的辅助手段。
2. 在以往的 Position Embedding 中,基本都是根据任务训练出来的向量。而 Google 直接给出了一个构造 Position Embedding 的公式:
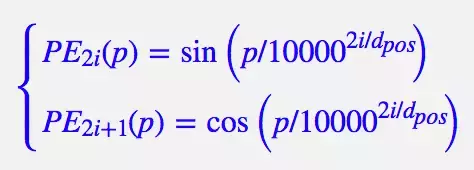
请点击此处输入图片描述
这里的意思是将 id 为 p 的位置映射为一个 dpos 维的位置向量,这个向量的第 i 个元素的数值就是 PEi(p)。
Google 在论文中说到他们比较过直接训练出来的位置向量和上述公式计算出来的位置向量,效果是接近的。因此显然我们更乐意使用公式构造的 Position Embedding 了。
3. Position Embedding 本身是一个绝对位置的信息,但在语言中,相对位置也很重要,Google 选择前述的位置向量公式的一个重要原因如下:
由于我们有 sin(α+β)=sinα cosβ+cosα sinβ 以及 cos(α+β)=cosα cosβ−sinα sinβ,这表明位置 p+k 的向量可以表明位置 p 的向量的线性变换,这提供了表达相对位置信息的可能性。
结合位置向量和词向量有几个可选方案, 可以把它们拼接起来作为一个新向量,也可以把位置向量定义为跟词向量一样大小,然后两者加起来。
FaceBook 的论文用的是前者,而 Google 论文中用的是后者。直觉上相加会导致信息损失,似乎不可取,但 Google 的成果说明相加也是很好的方案。看来我理解还不够深刻。
一些不足之处
到这里,Attention 机制已经基本介绍完了。 Attention 层的好处是能够一步到位捕捉到全局的联系,因为它直接把序列两两比较(代价是计算量变为